机器人原理及控制技术第09章 静态力
第九章静态力ChapterⅨStaticForces9.1引言9.2力和力距的表示9.3坐标系之间的力变换9.4等效关节力矩9.5通过关节力矩判断负载质量9.6利用腕力传感器判断负载质量9.7本章小结9.1引言(Introduction)本章介绍静态力和力距的表示方法,以及它们在坐标系之间的变换和等效关节力矩的计算方法。以及通过关节力矩和利用腕力传感器确定机械手负载物体质量等问题。9.29.2力和力距的表示力和力距的表示(TheRepresentationofForcesandMoments)力和力距都是矢量,要相对于某个确定的坐标系来进行描述。矢量f表示力,矢量m表示力矩。力与力矩合在一起用...
相关推荐
-
政治理论应知应会 100 题

 2024-12-12 94
2024-12-12 94 -
第八章 实验八 测定金属的电阻率(同时练习使用螺旋测微器)

 2025-03-17 7
2025-03-17 7 -
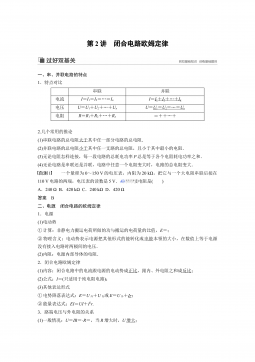
第八章 第2讲 闭合电路欧姆定律
 2025-03-17 9
2025-03-17 9 -
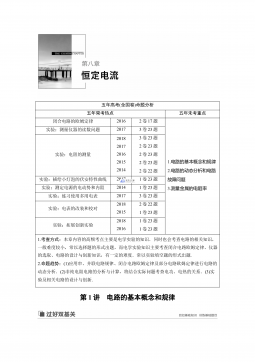
第八章 第1讲 电路的基本概念和规律
 2025-03-17 8
2025-03-17 8 -
第八章 本章综合能力提升练

 2025-03-17 4
2025-03-17 4 -
第八章 本章学科素养提升

 2025-03-17 9
2025-03-17 9 -
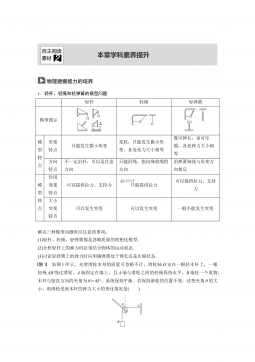
第二章 本章学科素养提升
 2025-03-17 8
2025-03-17 8 -
第九章 本章综合能力提升练

 2025-03-17 12
2025-03-17 12 -
高考物理总复习-高中全程训练计划-物理-课练 42 选修3-3、3-4(二)

 2025-03-17 12
2025-03-17 12 -
高考物理总复习-高中全程训练计划-物理-课练 41 选修3-3、3-4(一)

 2025-03-17 11
2025-03-17 11
作者详情
相关内容
-

第八章 本章学科素养提升
分类:高等教育
时间:2025-03-17
标签:无
格式:DOCX
价格:10 玖币
-

第二章 本章学科素养提升
分类:高等教育
时间:2025-03-17
标签:无
格式:DOCX
价格:10 玖币
-

第九章 本章综合能力提升练
分类:高等教育
时间:2025-03-17
标签:无
格式:DOCX
价格:10 玖币
-

高考物理总复习-高中全程训练计划-物理-课练 42 选修3-3、3-4(二)
分类:高等教育
时间:2025-03-17
标签:无
格式:DOC
价格:10 玖币
-

高考物理总复习-高中全程训练计划-物理-课练 41 选修3-3、3-4(一)
分类:高等教育
时间:2025-03-17
标签:无
格式:DOC
价格:10 玖币




 渝公网安备50010702506394
渝公网安备50010702506394
